Geographic Coordinates
One of the oldest systematic methods of location is based upon the geographic coordinate system. By drawing a set of east-west rings around the globe (parallel to the equator), and a set of north-south rings crossing the equator at right angles and converging at the poles, a network of reference lines is formed from which any point on the earth's surface can be located.
a. The distance of a point north or south of the equator is known as its latitude. The rings around the earth parallel to the equator are called parallels of latitude or simply parallels. Lines of latitude run east-west but north-south distances are measured between them.
b. A second set of rings around the globe at right angles to lines of latitude and passing through the poles is known as meridians of longitude or simply meridians. One meridian is designated as the prime meridian. The prime meridian of the system we use runs through Greenwich, England and is known as the Greenwich meridian. The distance east or west of a prime meridian to a point is known as its longitude. Lines of longitude (meridians) run north-south but east-west distances are measured between them (Figures 4-1 and 4-2).
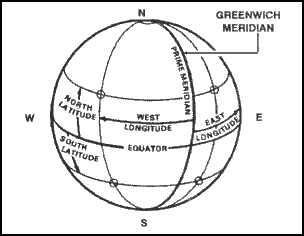
Figure 4-1. Prime meridian and equator.
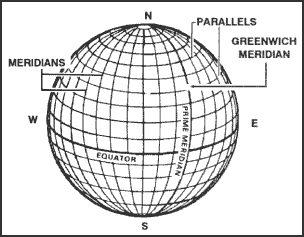
Figure 4-2. Reference lines.
c. Geographic coordinates are expressed in angular measurement. Each circle is divided into 360 degrees, each degree into 60 minutes, and each minute into 60 seconds. The degree is symbolized by ° , the minute by ′, and the second by ″. Starting with 0° at the equator, the parallels of latitude are numbered to 90° both north and south. The extremities are the north pole at 90° north latitude and the south pole at 90° south latitude. Latitude can have the same numerical value north or south of the equator, so the direction N or S must always be given. Starting with 0° at the prime meridian, longitude is measured both east and west around the world. Lines east of the prime meridian are numbered to 180° and identified as east longitude; lines west of the prime meridian are numbered to 180° and identified as west longitude. The direction E or W must always be given. The line directly opposite the prime meridian, 180° , may be referred to as either east or west longitude. The values of geographic coordinates, being in units of angular measure, will mean more if they are compared with units of measure with which we are more familiar. At any point on the earth, the ground distance covered by one degree of latitude is about 111 kilometers (69 miles); one second is equal to about 30 meters (100 feet). The ground distance covered by one degree of longitude at the equator is also about 111 kilometers, but decreases as one moves north or south, until it becomes zero at the poles. For example, one second of longitude represents about 30 meters (100 feet) at the equator; but at the latitude of Washington, DC, one second of longitude is about 24 meters (78 feet). Latitude and longitude are illustrated in Figure 4-3.
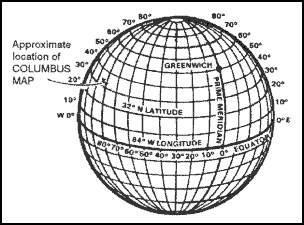
Figure 4-3. Latitude and longitude.
d. Geographic coordinates appear on all standard military maps; on some they may be the only method of locating and referencing a specific point. The four lines that enclose the body of the map (neatlines) are latitude and longitude lines. Their values are given in degrees and minutes at each of the four corners. On a portion of the Columbus map (Figure 4-4), the figures 32° 15' and 84° 45' appear at the lower right corner. The bottom line of this map is latitude 32° 15'00″N, and the line running up the right side is longitude 84° 45'00"W. In addition to the latitude and longitude given for the four corners, there are, at regularly spaced intervals along the sides of the map, small tick marks extending into the body of the map. Each of these tick marks is identified by its latitude or longitude value. Near the top of the right side of the map is a tick mark and the number 20'. The full value for this tick marks is 32° 20'00" of latitude. At one-third and two-thirds of the distance across the map from the 20' tick mark will be found a cross tick mark (grid squares 0379 and 9679) and at the far side another 20' tick mark. By connecting the tick marks and crosses with straight lines, a 32° 20'00" line of latitude can be added to the map. This procedure is also used to locate the 32° 25'00" line of latitude. For lines of longitude, the same procedure is followed using the tick marks along the top and bottom edges of the map.
e. After the parallels and meridians have been drawn, the geographic interval (angular distance between two adjacent lines) must be determined. Examination of the values given at the tick marks gives the interval. For most maps of scale 1:25,000, the interval is 2'30". For the Columbus map and most maps of scale 1:50,000, it is 5'00". The geographic coordinates of a point are found by dividing the sides of the geographic square in which the point is located into the required number of equal parts. If the geographic interval is 5'00" and the location of a point is required to the nearest second, each side of the geographic square must be divided into 300 equal parts (5'00" = 300"), each of which would have a value of one second. Any scale or ruler that has 300 equal divisions and is as long as or longer than the spacing between the lines may be used.
f. The following steps will determine the geographic coordinates of Wilkinson Cemetery (northwest of the town of Cusseta) on the Columbus map.
(1) Draw the parallels and meridians on the map that encloses the area around the cemetery.
(2) Determine the values of the parallels and meridians where the point falls.
Latitude 32° 15'00" and 32° 20'00".
Longitude 84° 45'00" and 84° 50'00".
(3) Determine the geographic interval (5'00" = 300").
(4) Select a scale that has 300 small divisions or multiples thereof (300 divisions, one second each; 150 divisions, two seconds each; 75 divisions, four seconds each, and so forth).
(5) To determine the latitude—
(a) Place the scale with the 0 of the scale on the latitude of the lowest number value (32° 15'00") and the 300 of the scale on the highest numbered line (32° 20'00") (1, Figure 4-4).
(b) While keeping the 0 and 300 on the two lines, slide the scale (2, Figure 4-4) along the parallels until the Wilkinson Cemetery symbol is along the edge of the numbered scale.
(c) Read the number of seconds from the scale (3, Figure 4-4), about 246.
(d) Convert the number of seconds to minutes and seconds (246" = 4'06") and add to the value of the lower numbered line (32° 15'00" + 4'06" = 32° 19'06") (4, Figure 4-4).
RESULTS:
- The latitude is 32° 19'06", but this is not enough.
- The latitude 32° 19'06" could be either north or south of the equator, so the letter N or S must be added to the latitude. To determine whether it is N or S, look at the latitude values at the edge of the map and find the direction in which they become larger. If they are larger going north, use N; if they are larger going south, use S.
- The latitude for the cemetery is 32° 19'06"N.
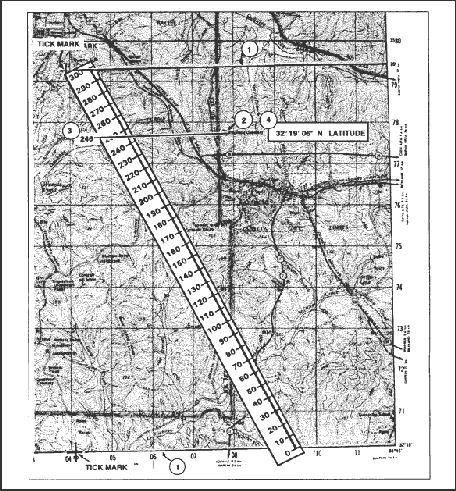
Figure 4-4. Determining latitude.
(6) Determine the longitude, repeat the same steps but measure between lines of longitude and use E and W. The geographic coordinates of Wilkinson Cemetery should be about 32° 19'06"N and 84° 47'32"W (Figure 4-5).
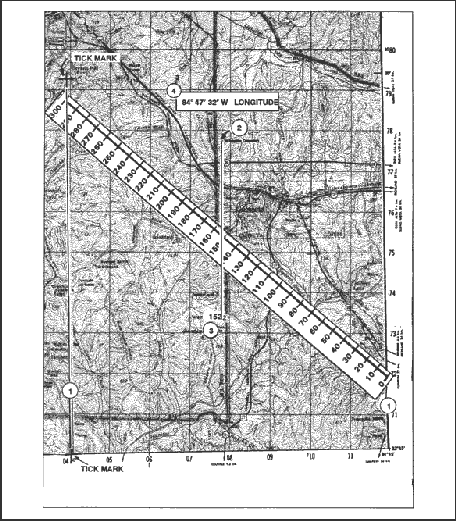
Figure 4-5. Determining longitude.
g. To locate a point on the Columbus map (Figure 4-6) when knowing the geographic coordinates, many of the same steps are followed. To locate 32° 25'28"N and 84° 50'56"W, first find the geographic lines within which the point falls: latitude 32° 25'00" and 32° 30'0"; and longitude 84° 50'00" and 84° 55'00". Subtract the lower latitude/longitude from the higher latitude/longitude.
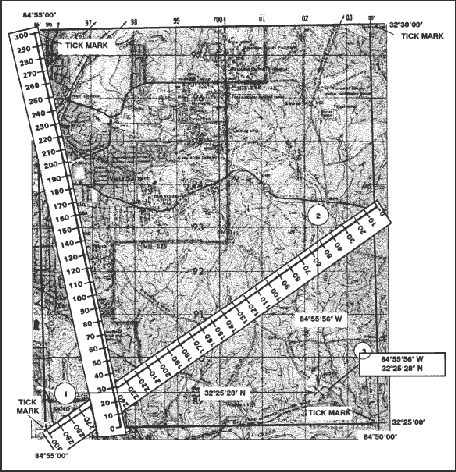
Figure 4-6. Determining geographic coordinates.
(1) Place the 0 of the scale on the 32° 25'00" line and the 300 on the 32° 30'00". Make a mark at the number 28 on the scale (the difference between the lower and higher latitude).
(2) Place the 0 of the scale on the 84° 50′00″ line and the 300 on the 84° 50′55″. Make a mark at the number 56 on the scale (the difference between the lower and higher longitude.
(3) Draw a vertical line from the mark at 56 and a horizontal line from the mark at 28; they intersect at 32 25’28"N and 84 50’56"W.
h. If you do not have a scale or ruler with 300 equal divisions or a map whose interval is other than 5'00", use the proportional parts method. Following the steps determines the geographic coordinates of horizontal control station 141.
(1) Locate horizontal control station 141 in grid square (GL0784) (Figure 4-7).
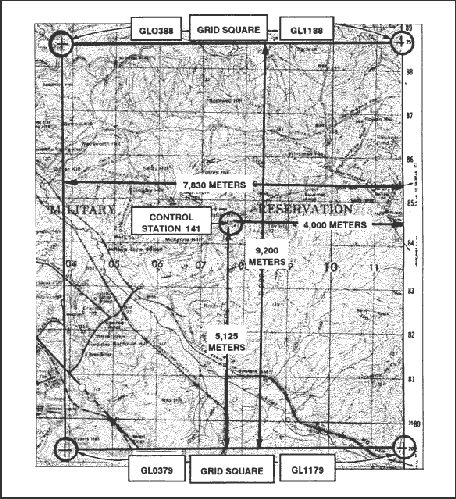
Figure 4-7. Using the proportional parts method.
(2) Find a cross in grid square GL0388 and a tick mark in grid square GL1188 with 25'.
(3) Find another cross in grid square GL0379 and a tick mark in grid square GL1179 with 20'.
(4) Enclose the control station by connecting the crosses and tick marks. The control station is between 20' and 25' (Figure 4-7).
(5) With a boxwood scale, measure the distance from the bottom line to the top line that encloses the area around the control station on the map (total distance) (Figure 4-7).
(6) Measure the partial distance from the bottom line to the center of the control station (Figure 4-7). These straight-line distances are in direct proportion to the minutes and seconds of latitude and are used to set up a ratio.
RESULTS:
- The total distance is 9,200 meters, and the partial distance is 5,125 meters (Figure 4-7).
- With the two distances and the five-minute interval converted to seconds (300"), determine the minutes and seconds of latitude using the following formula:
- 5,125 x 300 = 1,537,500
- 1,537,500 ÷ 9,200 = 167
- 167 ÷ 60 = 2'47"
- Add 2'47" to 32° 20'00" = 32° 20'47"
(7) Follow the same procedures to determine minutes and seconds of longitude (Figure 4-7).
RESULTS:
- The total distance is 7,830 meters, and the partial distance is 4,000 meters (Figure 4-7).
- 4,000 x 300 = 1,200,000
- 1,200,000 ÷ 7,830 = 153
- 153 ÷ 60 = 2'33"
- Add 2'33" to 84° 45' = 84° 47'33"N
(8) The geographic coordinates of horizontal control station 141 in grid square GL0784 are 32° 22'47"N latitude and 84° 47'33"W longitude.
| NOTE: |
When computing formulas, round off totals to the nearest whole number in step 2. In step 3, convert the fraction to seconds by multiplying the fraction by 60 and rounding off if the total is not a whole number. |
i. The maps made by some nations do not have their longitude values based on the prime meridian that passes through Greenwich, England. Table 4-1 shows the prime meridians that may be used by other nations. When these maps are issued to our soldiers, a note usually appears in the marginal information giving the difference between our prime meridian and the one used on the map.
| Amsterdam, Netherlands |
4° 53’01"E |
| Athens, Greece |
23° 42’59"E |
| Batavia (Djakarta), Indonesia |
106° 48’28"E |
| Bern, Switzerland |
7° 26’22"E |
| Brussels, Belgium |
4° 22’06"E |
| Copenhagen, Denmark |
12° 34’40"E |
| Ferro (Hierro), Canary Islands |
17° 39’46"W |
| Helsinki, Finland |
24° 53’17"E |
| Istanbul, Turkey |
28° 58’50"E |
| Lisbon, Portugal |
9° 07’55"W |
| Madrid, Spain |
3° 41’15"W |
| Oslo, Norway |
10° 43’23"E |
| Paris, France |
2° 20’14"E |
| Pulkovo, Russia |
30° 19’39"E |
| Rome, Italy |
12° 27’08"E |
| Stockholm, Sweden |
18° 03’30"E |
| Tirane, Albania |
19° 46’45"E |
Table 4-1. Table of prime meridians.
Back to Grids
|

